Answer:
(a)
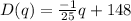
(b)

(c)
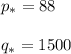
Explanation:
(a) For the demand equation D(q) we have
P1: 138 Q1: 250
P2: 108 Q2: 1000
We can find m, which is the slope of the demand equation,
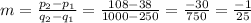
and then we find b, which is the point where the curve intersects the y axis.
We can do it by plugging one point and the slope into the line equation form:

With b: 148 and m: -1/25 we can write our demand equation D(q)
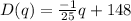
(b) to find the supply equation S(q) we have
P1: 102 Q1: 2200
P2: 102 Q2: 700
Similarly we find m, and b
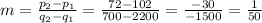

And we can write our Supply equation S(q):

(c) Now we may find the equilibrium quantity q* and the equilibrium price p* by writing D(q)=S(q), which means the demand equals the supply in equilibrium:
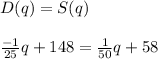
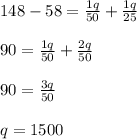
We plug 1500 as q into any equation, in this case S(q) and we get:

Which is the equilibrium price p*.