Answer:
Two public works employees are installing a wheelchair ramp near the steps of a public library. The length of the ramp is 25.51 feet.
Solution:
Consider the diagram attached below.
Let AB be ground. C be the position of main door.
As horizontal distance of the ramp = 24.8 feet
So AB = 24.8 feet
Main door of the library is 6 feet off the ground.
So CB = 6 feet
Need to calculate length of the ramp that is AC.
By Pythagoras theorem, square of one side of a right triangle is equal to sum of square of other two sides.
On applying Pythagoras theorem in right triangle ABC, we get
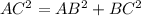
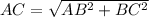
On substituting value of AB and BC,
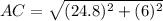
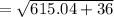
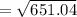
= 25.51 feet
Hence length of the ramp is 25.51 feet.