Question

The results of Accounting Principals’ latest Workonomix survey indicate the average American worker spends $1092 on coffee annually (the Consumerist, January 20, 2012). To determine if there are any differences in coffee expenditures by age group, samples of 10 consumers were selected for three age groups (18–34, 35–44, and 45 and Older). The dollar amount each consumer in the sample spent last year on coffee is provided below.

18-34 1355 969 1135 115 434 956 1456 1792 400 2045
35-44 1500 1374 1621 1277 1244 994 1056 825 1937 1922
45 and Older 763 1200 1350 1192 1567 1586 1305 1390 1415 1510
(a) Compute the mean, variance, and standard deviation for the each of these three samples.
(b) What observations can be made based on these data?

Answer 1

a)

Group 18-34 years old

`\bar x = 1041.625 \\ s^2=485301 \\ s=696.635`

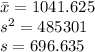
Group 35-44 years old

`\bar x = 1359.5 \\ s^2=178548 \\ s=422.549`

Group 45 and older

`\bar x = 1414.375 \\ s^2=18292.27 \\ s=135.248`

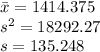
b)

According to the sample there is 9.04% probability that a person between 18 and 34 consume less than the average, 47.74% probability that a person between 35 and 44 consume more than the average and 50% probability that a person older than 45 consume more than the average.

Explanation:

a)

The mean for each sample is

`\bar x=(\sum_(k=1)^(10)x_k)/(10)`

where the
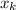`x_k` are the data corresponding to each group

The variance is

`s^2=(\sum_(k=1)^(10)(\bar x-x_k)^2)/(9)`

and the standard deviation is s, the square root of the variance.

Group 18-34 years old

`\bar x = 1041.625 \\ s^2=485301 \\ s=696.635`

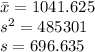
Group 35-44 years old

`\bar x = 1359.5 \\ s^2=178548 \\ s=422.549`

Group 45 and older

`\bar x = 1414.375 \\ s^2=18292.27 \\ s=135.248`

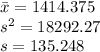
b)

Let's compare these averages against the general media established of $1,092 by using the corresponding z-scores

`z=(\bar x-\mu)/(s/√(n))`

where

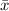`\bar x` = mean of the sample

`\mu` = established average

s = standard deviation of the sample

n = size of the sample

z-score of Group 18-34 years old

`z=(1041.625-1092)/(696.635/√(10))=-0.2286`

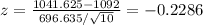
The area under the normal curve N(0;1) between -0.2286 and 0 is 0.0904. So according to the sample there is 9.04% probability that a person between 18 and 34 consume less than the average.

z-score of Group 35-44 years old

`z=(1359-1092)/(422.5491/√(10))=2.0019`

The area under the normal curve N(0;1) between 0 and 2.0019 is 0.4774. So according to the sample there is 47.74% probability that a person between 35 and 44 consume more than the average.

z-score of Group 45 and older

`z=(1414.375-1092)/(135.2489/√(10))=7.5375`

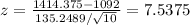
The area under the normal curve N(0;1) between 0 and 7.5375 is 0.5. So according to the sample there is 50% probability that a person older than 45 consume more than the average.