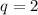Question

The demand equation for 6’ by 4’ outdoor garden shed is

D(q) = – 4q^2 – 2q + 1,500

where D(q) is the price in dollars at which q units are demanded. Find the quantity demanded in a day if the price of the shed is $1,480.

Answer 1

`q=2`

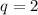
Explanation:

We need to find the quantity demanded if the price of the shed is 1480$. Hence:

`D(q)=1480=-4q^(2)-2q+1500`

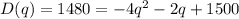
Sustract 1480 to both sides:

`-4q^(2) -2q+20=0`

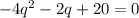
Multiply both sides by
`(-1)/(4)`

`q^(2)+(1)/(2)q-5=0`

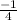
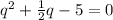
We have a quadratic equation, we can solve it using the cuadratic formula or simply factoring it:

`(q+(5)/(2))(q-2)`

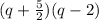
Now the solutions are given by:

`q_1=-(5)/(2) \\q_2=2`

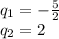
Since we look for a coherent answer we take the positive solution
`q_2`

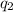
So the quantity demanded is
`q=2`