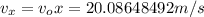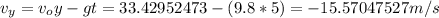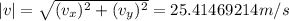Question

A projectile is launched with an initial speed of 39 m/s at an angle of 59° above the horizontal. What are the (a) magnitude and (b) angle of its velocity 2.0 s after launch (use the minus sign if the angle is below the horizontal)? What are the (c) magnitude and (d) angle of its velocity 5.0 s after launch (use the minus sign if the angle is below the horizontal)?

Answer 1

`t=2`

`|v|=24.38693565m/s\\\alpha =34.54737228$^(\circ)$`

`t=5`

`|v|=25.41469214m/s\\\alpha =-37.78183103$^(\circ)$`

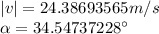
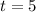
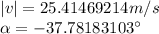
Step-by-step explanation:

Let's use projectile motion equations, but first lets find the components of the initial speed vector:

`v_ox=v_o*cos(\alpha _o)=39*cos(59)=20.08648492m/s`

`v_oy=v_o*sin(\alpha _o)=39*sin(59)=33.42952473m/s`

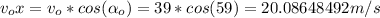
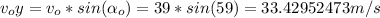
Now let's find the magnitude and the angle of the velocity at t=2s, asumming g=9.8.

`v_x=v_ox=20.08648492m/s`

`v_y=v_oy-gt=33.42952473-(9.8*2)=13.82952473m/s`

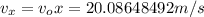
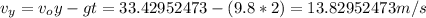
Now the magnitude is given by:

`|v|=\sqrt{(v_x)^(2) +(v_y)^(2)} =24.38693565m/s`

and its angle:

`\alpha =arctan((v_y)/(v_x) )=34.54737228$^(\circ)$`

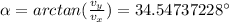
Similarlyfor t=5

`v_x=v_ox=20.08648492m/s`

`v_y=v_oy-gt=33.42952473-(9.8*5)=-15.57047527m/s`

`|v|=\sqrt{(v_x)^(2) +(v_y)^(2)} =25.41469214m/s`

`\alpha =arctan((v_y)/(v_x) )=-37.78183103$^(\circ)$`