Question

Suppose the ball is thrown from the same height as in the PRACTICE IT problem at an angle of 39.0° below the horizontal. If it strikes the ground 41.8 m away, find the following. (Hint: For part (a), use the equation for the x-displacement to eliminate v0t from the equation for the y-displacement.) (a) the time of flight s (b) the initial speed m/s (c) the speed and angle of the velocity vector with respect to the horizontal at impact speed m/s angle ° below the horizontal

Answer 1

The data about the previous problem are missing: I found them online and attached here (see picture). The relevant missing data is just the height of the building, which is 45 meters.

(a) 1.51 s

The motion along the x-direction is uniform (constant speed), so the position along the x-direction is given by

`x(t) = (v_0 cos \theta) t`

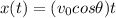
where
`v_0` is the initial speed,
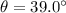`\theta=39.0^(\circ)` is the angle of launching, t is the time. We can re-write the formula as

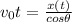`v_0 t = (x(t))/(cos \theta)` (1)

Along the y-direction the motion is accelerated (free-fall), so the equation for the vertical position is

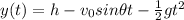`y(t)=h-v_0 sin \theta t -(1)/(2)gt^2` (2)

where h = 45.0 m is the height of the building and
`g=9.8 m/s^2` is the acceleration of gravity. Substituting (1) into (2),

`y(t)=h-x(t) tan \theta -(1)/(2)gt^2`

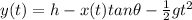
The ball strikes the ground when y(t)=0, so the equation becomes

`0=h-x(t) tan \theta -(1)/(2)gt^2`

And when this happens, the displacement along the x-axis is x = 41.8 m. Solving the equation for t and substituting the numbers, we find the time of flight:

`t=\sqrt{(2(h-xtan \theta))/(g)}=\sqrt{(2(45-41.8 tan 39^(\circ)))/(9.8)}=1.51 s`

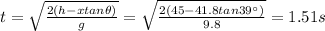
(b) 35.6 m/s

We can now easily find the initial speed by looking at the equation for the horizontal displacement:

`x(t) = (v_0 cos \theta) t`

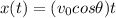
Re-arranging it,

`v_0=(x(t))/(t cos \theta)`

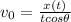
And substituting:

x = 41.8 m

t = 1.51 s

`\theta=39.0^(\circ)`

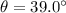
we find

`v_0 = (41.8)/((1.51)(cos 39.0^(\circ)))=35.6 m/s`

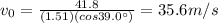
(c) 46.4 m/s at
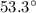`53.3^(\circ)` degrees below the horizontal

The horizontal component of the velocity during the whole motion is constant, so it is

`v_x = v_0 cos \theta = (35.6)(cos 39.0^(\circ))=27.7 m/s`

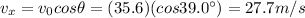
The vertical velocity instead follows the equation

`v_y(t) = -v_0 sin \theta -gt`

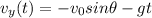
where the negative signs means the direction is downward. Substituting t=1.51 s, we find the vertical velocity at the time of impact:

`v_y =-(35.6)(sin 39.0^(\circ))-(9.8)(1.51)=-37.2 m/s`

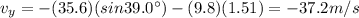
Therefore, the speed at the moment of impact is:

`v=√(v_x^2+v_y^2)=√((27.7)^2+(-37.2)^2)=46.4 m/s`

And the direction will be given by

`\theta = tan^(-1)((v_y)/(v_x))=tan^(-1)((-37.2)/(27.7))=-53.3^(\circ)`