Question

stanford Polynomial differentiation. Suppose p is a polynomial of degree n − 1 or less, given by p(t) = c1 + c2t + · · · + cntn−1. Its derivative (with respect to t) p′(t) is a polynomial of degree n−2 or less, given by p′(t) = d1 +d2t+···+dn−1tn−2. Find a matrix D for which d = Dc. (Give the entries of D, and be sure to specify its dimensions.)

Answer 1

The matrix representation of the linear transformation is

`\begin{pmatrix} 0 & 1 & 0 & 0 & \cdots & 0\\ 0 & 0 & 2 & 0 & \cdots & 0\\ 0 & 0 & 0 & 3 & \cdots & 0\\ \cdot & \cdot & \cdot & \cdot & \cdots & \cdot\\ 0 & 0 & 0 & 0 & \cdots & n-1\\ 0 & 0 & 0 & 0 & \cdots & 0\end{pmatrix}`,

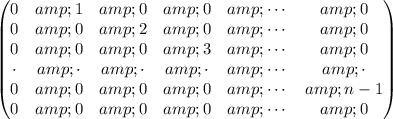which is a matrix of dimension
`n* n`.

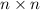Explanation:

First, as we are working with vector spaces, in particular with
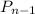`P_(n-1)` the space of real polynomials of degree at most n-1, we need to set a base. As usual we will use the canonical base:
`\{1,t,t^2,\ldots,t^(n-1)\}`.

The differential operator
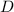`D` is such that
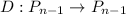`D:P_(n-1)\rightarrow P_(n-1)`. So, in the image we will use the canonical base too.

Recall that, if we have a polynomial
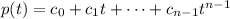`p(t) = c_0 + c_1t + \cdots +c_(n-1)t^(n-1)`, its derivative is
`p'(t) =  c_1 + 2c_2t +\cdots +(n-1)c_(n-1)t^(n-2)`, i.e.
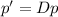`p' = Dp`. In order to construct the matrix representation of a linear transformation we must evaluate the transformation at the elements of the base. In this case we must find

`\{D1, Dt, Dt^2,\ldots, Dt^(n-1)\}`.

It is no difficult to notice that

`\{D1, Dt, Dt^2,\ldots, Dt^(n-1)\} = \{0, 1, 2t, \ldtos, (n-1)t^(n-2)\}.`

The next step is to write the image of each element of the base as a linear combination of the base of
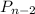`P_(n-2)`. Then,

`0 = 0*1+0*t+\cdots + 0*t^(n-2)`

`1 = 1*1+0*t+\cdots + 0*t^(n-2)`

`2t = 0*1+2*t+\cdots + 0*t^(n-2)`

`3t^2 = 0*1+0*t+3t^2+\cdots + 0*t^(n-2)`

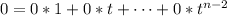
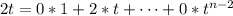
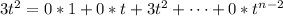
and so on, until

`0 = 0*1+0*t+\cdots + (n-1)*t^(n-2)`.

The coefficients of this linear combinations are written as columns of matrix, which is the representation we are looking for:

`\begin{pmatrix} 0 & 1 & 0 & 0 & \cdots & 0\\ 0 & 0 & 2 & 0 & \cdots & 0\\ 0 & 0 & 0 & 3 & \cdots & 0\\ \cdot & \cdot & \cdot & \cdot & \cdots & \cdot\\ 0 & 0 & 0 & 0 & \cdots & n-1\\ 0 & 0 & 0 & 0 & \cdots & 0\end{pmatrix}`.

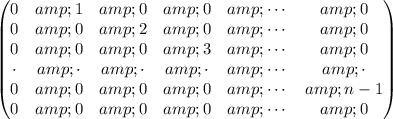In this case we have a matrix of dimension
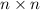`n* n`, because we are considering a linear transformation from
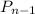`P_(n-1)` to itself, rather to
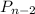`P_(n-2)`.