Question

g A proton moves at 3.60 105 m/s in the horizontal direction. It enters a uniform vertical electric field with a magnitude of 9.40 103 N/C. Ignore any gravitational effects. (a) Find the time interval required for the proton to travel 4.00 cm horizontally. ns (b) Find its vertical displacement during the time interval in which it travels 4.00 cm horizontally. (Indicate direction with the sign of your answer.) mm (c) Find the horizontal and vertical components of its velocity after it has traveled 4.00 cm horizontally.

Answer 1

Step-by-step explanation:

It is given that,

Speed of the proton,
`v=3.6* 10^5\ m/s`

Electric field,
`E=9.4* 10^3\ N/C`

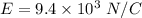
(a) Distance covered, d = 4 cm = 0.04 m

Let t is the time interval required for the proton to travel 4.00 cm horizontally. It can be calculated as :

`t=(d)/(v)`

`t=(0.04)/(3.6* 10^5)`

`t=1.11* 10^(-7)\ s`

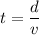
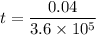
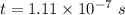
or

t = 111 ns

(b) Since, initial speed = 0 in vertical direction. So,

So, q E = ma

`a_y=(E_yq)/(m)`

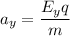
Displacement is given by :

`y=ut+(1)/(2)a_yt^2`

`y=(1)/(2)(E_yq)/(m)t^2`

`y=(1)/(2)* (9.4* 10^3* 1.67* 10^(-19))/(1.67* 10^(-27))(1.11* 10^(-7))^2`

`y=0.00579\ m`

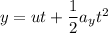
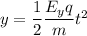
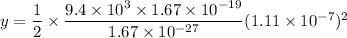
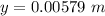
(c) For vertical component of velocity, use equation of kinematics as :

`v_y^2-u^2=2a_yd` (d = 4 cm)

`v=\sqrt{2(E_yq)/(m)d_y}`

`v=\sqrt{2* (9.4* 10^3* 1.67* 10^(-19))/(1.67* 10^(-27))* 0.04}`

`v=2.74* 10^5\ m/s`

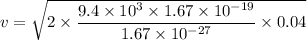
For horizontal component of velocity,

`v_x=(d)/(t)`

`v_x=(0.04)/(1.11* 10^(-7))`

`v_x=3.6* 10^5\ m/s`

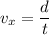
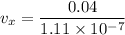
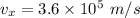
Hence, this is the required solution.