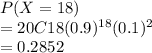Question

A certain drug treatment cures 90% of cases of hookworm in children.18 Suppose that 20 children suffer- ing from hookworm are to be treated, and that the chil- dren can be regarded as a random sample from the population. Find the probability that (a) all 20 will be cured. (b) all but 1 will be cured. (c) exactly 18 will be cured. (d) exactly 90% will be cured.

Answer 1

Explanation:

Here X the no of children suffering from hookworm treated and recovered is binomial because

a) Each child is independent of the other

b) There are only two outcomes

c) The probability for any child to recover is constant as 90% = 0.9

X is Bin (20,0.9)

a) Prob that all 20 will be cured

=P(X=20)=
`0.9^(20) \\=0.1216`

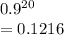
b) Prob all but 1 will be cured=
`P(x=1) = 20C1 (0.9) (.1)^(19) \\=1.8(10^8)`

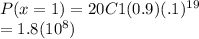
c) Prob exactly 18 will be cured

`=P(X=18)\\=20C18 (0.9)^(18) (0.1)^2\\= 0.2852`

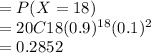
d) Prob exactly 90% will be cured.

=
`P(X=18)\\=20C18 (0.9)^(18) (0.1)^2\\= 0.2852`