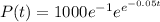Answer:
The solution is
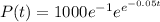 .
.
Explanation:
We have the Gompertz's differential equation
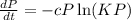 .
.
Notice that this a separable equation. So,
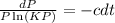 .
.
Now, integrating in both sides:
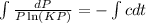 .
.
Recall that
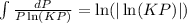 .
.
Thus,
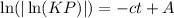 ,
,
and taking exponential:
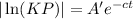 .
.
Taking another exponential
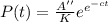 .
.
Now, let us substitute the given values for c and K:
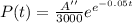 .
.
To find the value of the constant A'' we use the initial condition:
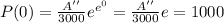 .
.
Then,
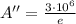 .
.
Hence, the solution is