Question

Balance the given chemical equation. Potassium superoxide and carbon dioxide react to form potassium carbonate and oxygen:

KO2 + CO2 → K2CO3 + O2

(Write the reaction in the form x1KO2 + x2CO2 → x3K2CO3 + x4O2, and solve for x1, x2, x3, and x4.)

Answer 1

`\left[\begin{array}{ccc}x1\\x2\\x3\\x4\end{array}\right] =\left[\begin{array}{ccc}4\\2\\2\\3\end{array}\right]`

4KO2 + 2CO2 → 2K2CO3 + 3O2

Explanation:

First we write the reaction in the asked form :

x1 KO2 + x2 CO2 → x3 K2CO3 + x4 O2

In a chemical equation, tha amount of substance that react is the same amount that is formed :

On each side of the equation we must have the same amount of K,C and O.

Let's write this in equations :

K balance :
`x1 =2x3`

C balance :
`x2=x3`

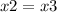
O balance :
`2x1+2x2=3x3+2x4`

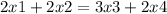
The linear equations system is :

`x1=2x3\\2x1+2x2=3x3+2x4\\x2=x3`

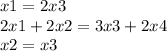
Let's equal to 0 to obtain a homogeneous equations system (for convenience) :

`x1-2x3=0\\2x1+2x2-3x3-2x4=0\\x2-x3=0`

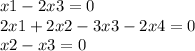
Let's work with the extended system matrix :

`\left[\begin{array}{ccccc}1&0&-2&0&0\\2&2&-3&-2&0\\0&1&-1&0&0\end{array}\right]`

Working with the matrix :
`\left[\begin{array}{ccccc}1&0&-2&0&0\\0&2&1&-2&0\\0&1&-1&0&0\end{array}\right]`

→

`\left[\begin{array}{ccccc}1&0&-2&0&0\\0&1&1/2&-1&0\\0&1&-1&0&0\end{array}\right]`

→
`\left[\begin{array}{ccccc}1&0&-2&0&0\\0&1&-1&0&0\\0&1&1/2&-1&0\end{array}\right]`

→
`\left[\begin{array}{ccccc}1&0&-2&0&0\\0&1&-1&0&0\\0&0&3/2&-1&0\end{array}\right]`

→
`\left[\begin{array}{ccccc}1&0&-2&0&0\\0&1&-1&0&0\\0&0&1&-2/3&0\end{array}\right]`

→
`\left[\begin{array}{ccccc}1&0&0&-4/3&0\\0&1&0&-2/3&0\\0&0&1&-2/3&0\end{array}\right]`

The matrix is extended to the following linear system :

`x1-(4)/(3) x4=0\\x2-(2)/(3) x4=0\\x3-(2)/(3) x4=0`

`x1=(4)/(3)x4\\ x2=(2)/(3) x4\\x3=(2)/(3)x4`

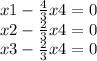
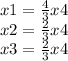
`\left[\begin{array}{c}x1&x2&x3&x4\end{array}\right] =\left[\begin{array}{c}(4)/(3) x4&(2)/(3)x4 &(2)/(3)x4 &x4\end{array}\right]`

`\left[\begin{array}{c}(4)/(3)&(2)/(3)&(2)/(3)&1   \end{array}\right] x4=\left[\begin{array}{c}(4)/(3)&(2)/(3)&(2)/(3)&1   \end{array}\right]t`

t∈ IR

Let's choose t=3 to eliminate the fractional numbers →

`\left[\begin{array}{c}x1&x2&x3&x4\end{array}\right] = \left[\begin{array}{c}4&2&2&3\end{array}\right]`