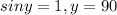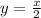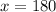Question

5cosx -2sin(x/2) +7=0
Help me to find x step by step
pls​

Answer 1

x = 180

Explanation:

First, you need to know

1. Double-angle formula:

cos(2x) =
`cos^(2)x - sin^(2)x`

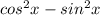
2. Pythagorean identity:

`cos^(2)x + sin^(2)x = 1`

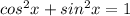
Back to your problem, replacing the variable by the above:

`5cosx-sin(x)/(2)+7 = 0`

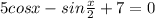
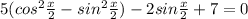`5(cos^(2)(x)/(2)-sin^(2)(x)/(2)) - 2sin(x)/(2) + 7 = 0` By Double-angle formula

`5(1 - 2sin^(2)(x)/(2)) - 2sin(x)/(2) + 7 = 0` By Pythagorean identity

Given
`y = (x)/(2)`

`5(1-2sin^(2)y) - 2siny + 7 = 0`

`10sin^(2)y+2siny-12=0`

`5sin^(2)y+siny-6=0`

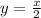
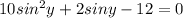
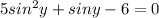
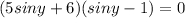`(5siny + 6)(siny - 1)=0`, we know -1 < sinx < 1, for every x ∈ R

`siny = 1, y =90`

`y = (x)/(2)`

`x = 180`