Question

What partial pressure of C2H4 gas (in mm Hg) is required to maintain a solubility of 4.92×10-2 g/L in water at 25 °C? kH for C2H4 at 25 °C is 4.78×10-3 mol/L·atm.

Answer 1

Answer: The partial pressure of
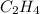`C_2H_4` is 281 mmHg

Step-by-step explanation:

We are given:

Solubility of ethene gas =
`4.92* 10^(-2)g/L`

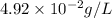
To convert this solubility into mol/L, we divide the given solubility by the molar mass of the gas, which is 28 g/mol

`\text{Solubility (in mol/L)}=\frac{\text{Solubility (in g/L)}}{\text{Molar mass}}`

`\text{Solubility (in mol/L)}=(4.92* 10^(-2)g/L)/(28g/mol)=0.176* 10^(-2)mol/L`

To calculate the molar solubility, we use the equation given by Henry's law, which is:

`C_(C_2H_4)=K_H* p_(C_2H_4)`

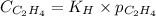
where,

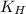`K_H` = Henry's constant =
`4.78* 10^(-3)mol/L.atm`

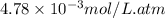
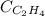`C_(C_2H_4)` = molar solubility of ethene gas =
`0.176* 10^(-2)mol/L`

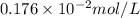
Putting values in above equation, we get:

`0.176* 10^(-2)mol/L=4.78* 10^(-3)mol/L.atm* p_(C_2H_4)\\\\p_(C_2H_4)=(0.176* 10^(-2)mol/L)/(4.78* 10^(-3)mol/L.atm)=0.370atm`

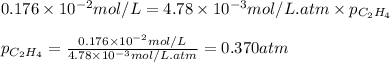
Converting this into mmHg, we use the conversion factor:

1 atm = 760 mmHg

So,
`0.370atm* (760mmHg)/(1atm)=281mmHg`

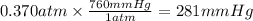
Hence, the partial pressure of
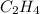`C_2H_4` is 281 mmHg