Answer:
45.6 m at
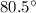 south of west
south of west
Step-by-step explanation:
Let's take the north-south direction as y-direction (with south being positive) and east-west direction as x-direction (with west being positive). Therefore, the two components of Cody's motion are:
-
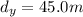 (south)
(south)
-
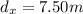 (west)
(west)
Since they are perpendicular, the magnitude of the net displacement can be calculated by using Pythagorean's theorem:
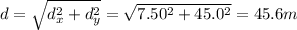
The direction instead can be measured as follows:
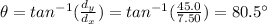
And given the convention we have used, this angle is measured as south of west.