Answer:
The probability that the student is going to pass the test is 0.0545
Explanation:
The variable that says the number of correct questions follows a Binomial distribution, because there are n identical and independent events with a probability p of success and a probability 1-p of fail. So, the probability of get x questions correct is:

Where n is equal to 10 questions and p is the probability of get a correct answers, so p is equal to 1/2
Then, if the student pass the test with at least 8 questions correct, the probability P of that is:
P = P(8) + P(9) + P(10)
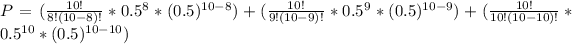
P = 0.0439 + 0.0097 + 0.0009
P = 0.0545