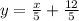Question

The given line passes through the points (0, ) and (2, 3). On a coordinate plane, a line goes through (0, negative 3) and (2, 3). A point is at (negative 1, negative 1). What is the equation, in point-slope form, of the line that is parallel to the given line and passes through the point ()?

Answer 1

`y=(x)/(5)+(12)/(5)`

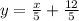
Explanation:

1) The Point-slope form equation is given in this form:

`(x-x_(0))=m(y-y_(0))`

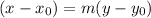
2)Looking at the given graph, we can pick two points: (-5,-4) and (0,-3)

3) Before using the Point-slope form We have to find out the slope:

`m=(-4-(-3))/(0-(-5)) \Rightarrow m=(-4+3)/(0+5) \Rightarrow m=(-1)/(5)`

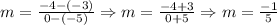
4)Parallel lines share the same slope. The one that passes through (-2,2) is found by calculating its linear parameter "b":

`y=(x)/(5)+b\Rightarrow 2=(-2)/(5)+b\\5*10=(-2+b)*5\Rightarrow 5b=12 \Rightarrow (5b)/(5) =(12)/(5) \Rightarrow b=(12)/(5)`

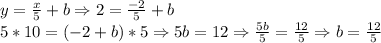
Then, the answer is:

`y=(x)/(5)+(12)/(5)`