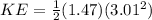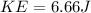Question

awhite billiard ball with mass mw = 1.47 kg is moving directly to the right with a speed of v = 3.01 m/s and collides elastically with a black billiard ball with the same mass mb = 1.47 kg that is initially at rest. The two collide elastically and the white ball ends up moving at an angle above the horizontal of θw = 68° and the black ball ends up moving at an angle below the horizontal of θb = 22°.

Answer 1

speed of white ball is 1.13 m/s and speed of black ball is 2.78 m/s

initial kinetic energy = final kinetic energy

`KE = 6.66 J`

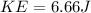
Step-by-step explanation:

Since there is no external force on the system of two balls so here total momentum of two balls initially must be equal to the total momentum of two balls after collision

So we will have

momentum conservation along x direction

`m_1v_(1i) + m_2v_(2i) = m_1v_(1x) + m_2v_(2x)`

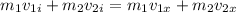
now plug in all values in it

`1.47 * 3.01 + 0 = 1.47 v_1cos68 + 1.47 v_2cos22`

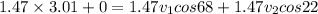
so we have

`3.01 = 0.375v_1 + 0.927v_2`

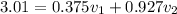
similarly in Y direction we have

`m_1v_(1i) + m_2v_(2i) = m_1v_(1y) + m_2v_(2y)`

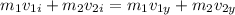
now plug in all values in it

`0 + 0 = 1.47 v_1sin68 - 1.47 v_2sin22`

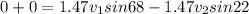
so we have

`0 = 0.927v_1 - 0.375v_2`

`v_2 = 2.47 v_1`

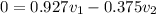
now from 1st equation we have

`3.01 = 0.375 v_1 + 0.927(2.47 v_1)`

`v_1 = 1.13 m/s`

`v_2 = 2.78 m/s`

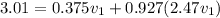
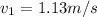
so speed of white ball is 1.13 m/s and speed of black ball is 2.78 m/s

Also we know that since this is an elastic collision so here kinetic energy is always conserved to

initial kinetic energy = final kinetic energy

`KE = (1)/(2)(1.47)(3.01^2)`

`KE = 6.66 J`