Answer:
The probability that the sample mean would differ from the population mean by greater than 2.2 kilograms is 0.0104 .
Explanation:
The mean weight of an adult is 62 kilograms with a variance of 144
i.e.
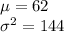
We are supposed to find probability that the sample mean would differ from the population mean by greater than 2.2 kilograms
i.e.
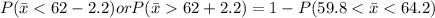
Using formula :
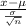
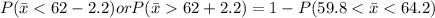
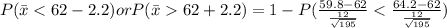
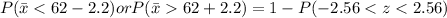

Refer the z table
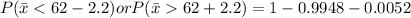
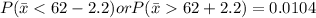
Hence The probability that the sample mean would differ from the population mean by greater than 2.2 kilograms is 0.0104 .