Question

Sixty percent of the eligible voting residents of a certain community support the incumbent candidate. If eight of the residents are selected at random, find the probability that at least five of the eight support the candidate.

Answer 1

By the binomial theorem we know that

`1 = (.4 + .6)^8 \\ = {8 \choose 0} (.4)^(8) (.6)^(0) + {8 \choose 1} (.4)^(7) (.6)^(1) +{8 \choose 2} (.4)^(6) (.6)^(2) + {8 \choose 3} (.4)^(5) (.6)^(3) + {8 \choose 4} (.4)^(4) (.6)^(4) \\ + \quad {8 \choose 5} (.4)^(3) (.6)^(5) + {8 \choose 6} (.4)^(2) (.6)^(6) + {8 \choose 7} (.4)^(1) (.6)^(7) + {8 \choose 8} (.4)^(0) (.6)^(8)`

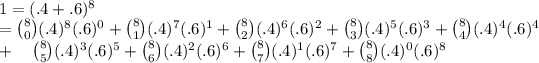
The probability that exactly 5 of 8 support the incumbent is the term

`{8 \choose 5} (.4)^(3) (.6)^(5)`

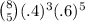
So at least five of eight support is the sum of this term and beyond,

`p={8 \choose 5} (.4)^(3) (.6)^(5) + {8 \choose 6} (.4)^(2) (.6)^(6) + {8 \choose 7} (.4)^(1) (.6)^(7) + {8 \choose 8} (.4)^(0) (.6)^(8)`

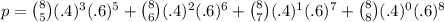
No particularly easy way of calculating that except popping it into Wolfram Alpha which reports

`p = ( 46413)/(78125)`

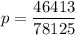
Shouldn't half the terms work out to .6 ? Interestingly it's not exactly .6 but pretty close at .594.