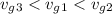Answer:
Second ball
Step-by-step explanation:
When a ball is thrown up with a certain velocity when the object reaches the same point from where it was thrown the velocity of the object becomes equal to the velocity with which the ball was thrown.
First ball
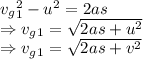
Second ball
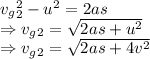
Third ball
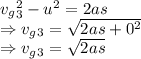
From the equations above it can be seen that the second ball will have the highest velocity when it hits the ground.
So,