Answer:
Hence, the probability that randomly selected thermometer reads greater than negative 0.69 is 0.7549
Explanation:
Consider the provided information.
The readings on thermometers are normally distributed with a mean of degrees and a standard deviation of 1.00 degrees.
That means the value of σ = 1.
We need to find the probability that a randomly selected thermometer reads greater than negative 0.69
That means the value of mean is 0.
Normal distribution =

Substitute the respective values as shown:
The probability should be greater that -0.6, Thus.
P(X>-0.6)=
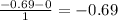
Now use the standard normal table to find the value of P(Z>-0.69)
P(X>-0.6)=0.7549
Hence, the probability that randomly selected thermometer reads greater than negative 0.69 is 0.7549
The required region is shown in figure 1.