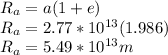Question

Suppose that a comet that was seen in 563 A.D. by Chinese astronomers was spotted again in year 1951. Assume the time between observations is the period of the comet and take its eccentricity as 0.986. What are (a) the semimajor axis of the comet's orbit and (b) its greatest distance from the Sun?

Answer 1

`a=2.77*10^(13)m`

`R_a=5.49*10^(13)m`

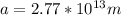
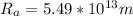
Step-by-step explanation:

The period of the comet is the time it takes to do a complete orbit:

T=1951-(-563)=2514 years

writen in seconds:

`2514years*(3,154*10^7s)/(1year)=7.93 *10^(10)s`

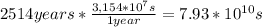
Since the eccentricity is greater than 0 but lower than 1 you can know that the trajectory is an ellipse.

Therefore, if the mass of the sun is aprox. 1.99e30 kg, and you assume it to be much larger than the mass of the comet, you can use Kepler's law of periods to calculate the semimajor axis:

`T^2=(4\pi^2)/(Gm_(sun))a^3\\ a=\sqrt[3]{(Gm_(sun)T^2)/(4\pi^2) } \\a=1.50*10^(6)m`

Then, using the law of orbits, you can calculate the greatest distance from the sun, which is called aphelion:

`R_a=a(1+e)\\R_a=2.77*10^(13)(1.986)\\R_a=5.49*10^(13)m`