Question

Calculate the value of a ​$1 comma 000​-par-value bond paying quarterly interest at an annual coupon interest rate of 13​% and having 12 years until maturity if the required return on​ similar-risk bonds is currently a 11​% annual rate paid quarterly.

Answer 1

The value of the bond = $1,132.37

Step-by-step explanation:

The price of a bond is equivalent to the present value of all the cash flows that are likely to accrue to an investor once the bond is bought. These cash-flows are the periodic coupon payments that are to be paid quarterly and the par value of the bond that will be paid at the end of 12 years.

During the 12 years, there are 48 equal periodic coupon payments that will be made. Given a par value equal to $1,000, in each year, the total coupon paid will be
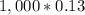`1,000*0.13`= $130. This annual payment will be split into four equal payments equal to
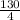`(130)/(4)` =$32,5 . This stream of cash-flows is an ordinary annuity.

The required rate of return is to 11% per annum which equates to 2.75% per quarterly period.

The PV of the cash-flows = PV of the coupon payments + PV of the par value of the bond

=32.5*PV Annuity Factor for 48 periods at 2.75%+ $1,000* PV Interest factor with i=2.75% and n =48

=
`32.5*([1-(1+0.0275)^-^4^8])/(0.0275)+ (1,000)/((1+0.0275)^4^8)`=$1,132.37