Question

To find the velocity and acceleration vectors for uniform circular motion and to recognize that this acceleration is the centripetal acceleration. Suppose that a particle's position is given by the following expression: r(t)=R[cos(ωt)i^+sin(ωt)j^] =Rcos(ωt)i^+Rsin(ωt)j^.The particle's motion can be described by ____________.(A) an ellipse starting at time t=0 on the positive x axis(B) an ellipse starting at time t=0 on the positive y axis(C) a circle starting at time t=0 on the positive x axis(D) a circle starting at time t=0 on the positive y axis

Answer 1

(C) a circle starting at time t=0 on the positive x axis

Step-by-step explanation:

particle's position is

r(t)=R[cos(ωt)i^+sin(ωt)j^] =Rcos(ωt)i^+Rsin(ωt)j^

this is a parametric equation of a circle, because the axis at x and y are the same = R.

for t=0:

r=Ri^

so: circle starting at time t=0 on the positive x axis

On the other hand:

`v=(dx)/(dt)= Rw[-sin(wt)i+cos(wt)j]\\a=(dv)/(dt)= Rw^(2)[-cos(wt)i-sin(wt)j]`

The value of the magnitude of the acceleration is:

`a=Rw^(2)(cos^(2)(wt)+sin^(2)(wt))=Rw^(2)`

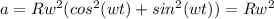
we can recognise that this represent the centripetal acceleration.