Question

An increased number of colleges have been using online resources to research applicants. According to a study from last​ year, 35​% of admissions officers indicated that they visited an applying​ student's social networking page. A random sample of 100 admissions officers was recently selected and it was found that 47 of them visit the social networking sites of students applying to their college. Using alphaequals0.10​, complete parts a and b below. a. Does this sample provide support for the hypothesis that the proportion of admissions officers who visit an applying​ students' social networking page has increased in the past​ year?

Determine the null and alternative hypotheses. Choose the correct answer below.

A. H0​: p=0.36 H1​: p≠0.36

B. H0​: p>0.36 H1​: p≤0.36

C. H0​: p≥0.36 H1​: p<0.36

D. H0​: p ≤0.36 H1​: p>0.36

Determine the critical​ value(s) of the test statistic.

zα=_____

​(Use a comma to separate answers as needed. Round to three decimal places as​ needed.)

Calculate the test statistic.

zp=_____

​(Round to two decimal places as​ needed.)

Determine the conclusion. Choose the correct answer below.

A.Do not reject H0. There is not sufficient evidence to support the hypothesis that the proportion of admissions officers who visit an applying​ students' social networking page has increased in the past year

B. Reject H0. There is not sufficient evidence to support the hypothesis that the proportion of admissions officers who visit an applying​ students' social networking page has increased in the past year

C.Do not reject H0. There is sufficient evidence to support the hypothesis that the proportion of admissions officers who visit an applying​ students' social networking page has increased in the past year

D. Reject H0. There is sufficient evidence to support the hypothesis that the proportion of admissions officers who visit an applying​ students' social networking page has increased in the past year

Answer 1

D. H0​: p ≤0.36 H1​: p>0.36

`$$(Right tail test) Z_(\alpha)=Z_(0.1)=1.28155`

`Z_p=-0.25516`

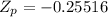
D. Reject H0. There is sufficient evidence to support the hypothesis that the proportion of admissions officers who visit an applying​ students' social networking page has increased in the past year

Explanation:

To solve this problem, we run a hypothesis test about the population proportion.

`$$Sample proportion: $\bar P=0.47\\Sample size n=100$\\Significance level \alpha=0.10$\\(Left tail test) Z_(1-\alpha)=Z_(0.90)=-1.28155$\\(Right tail test) Z_(\alpha)=Z_(0.1)=1.28155$\\(Two-tailed test) $Z_(1-\alpha/2)=Z_(0.95)=-1.64485$ and $ Z_(\alpha/2)=Z_(0.05)=1.64485\\\\`

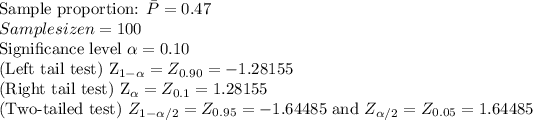
The appropriate hypothesis system for this situation is:

`H_0:\pi_0=0.35\\H_a:\pi_0 > 0.35\\\\$Proportion in the null hypothesis is:\\\pi_0=0.35\\\\`

`$$The test statistic is $Z=((\bar P-\pi_0)√(n))/(√(\pi_0(1-\pi_0)))\\$The calculated statistic is Z_c=((0.47-0.35)√(100))/(√(0.35(1-0.35)))=-0.25516\\p-value = P(Z \geq Z_c)=0.01620\\\\`

Since, the calculated statistic
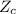`Z_c` is greater than critical
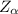`Z_(\alpha)`, the null hypothesis should be rejected. There is enough statistical evidence to state that the proportion of admissions officers who visit an applying​ students' social networking page has increased in the past year.