Question

g n some distant dystopian future on the surface of a war ravaged Mars, a rocket is launched from top of a weapons platform located 8 m above the ground at an angle of 30◦ above the horizontal and with an initial speed of 12 m/s. The rocket is equipped with a special propulsion system which provides a constant horizontal acceleration of 2 m/s2, t seconds after the rocket has been launched. Assuming a constant downward acceleration of 4 m/s2 due to gravity on Mars, give a vector-valued function r(t) (with a horizontal component and a vertical component) which represents the position of the rocket relative to the point on the ground directly below the launch point of the rocket t seconds after launch.

Answer 1

the vector position is r = (10.4 t + t²) i + (8+ 6t - 2 t²) j

Step-by-step explanation:

In this problem we have acceleration in the x and y axes, therefore we will use the accelerated motion equations

X = Xo + Vox t + ½ aₓ t²

Y = I + I go t + ½
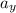`a_(y)` t²

We calculate the components of velocity using trigonometry

Vox = Vo cos θ = 12 cos 30

Voy = Voy sin θ = 12 sin 30

Vox = 10.4 m / s

Voy = 6 m / s

The value accelerations are data

aₓ = 2 m / s²

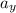`a_(y)` = - 4 m / s²

The initial position is

Xo = 0

Yo = 8 m

Since the launching point is 8 m above the ground. The acceleration is negative because it has a downward direction; with this data we write the equations of the position

X = 10.4 t + ½ 2 t²

Y = 8 + 6 t - ½ 4 t²

X = 10.4 t + t²

Y = 8 + 6 t - 2 t²

We write the position vector

r = x i + y j

r = (10.4 t + t²) i + (8+ 6t - 2 t²) j

this the vector position