Answer:
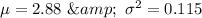
Explanation:
Given : The probability of a correct classification of any part is : p=0.96
sample size : n= 3
The formula to find the mean and variance for binomial distribution is given by :-
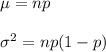
Let the random variable X denote the number of parts that are correctly classified.
The, for the given situation, we have
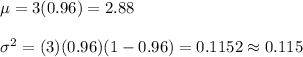
Hence, the mean and variance of X are 2.88 and 0.115 respectively.