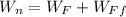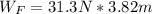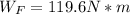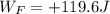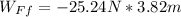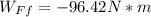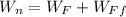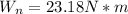Answer:
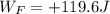 : Work done by horizontal force
: Work done by horizontal force
 : Work done by friction force
: Work done by friction force
 : Net work
: Net work
Step-by-step explanation:
Work theory
Work is the product of a force applied to a body and the displacement of the body in the direction of this force.
Thus. The work is equal to the product of the force by the distance (d) and by the cosine of the angle ( α) that exists between the direction of the force (F) and the direction that travels the point or the object that moves:
W= F*d*cosα Formula (1)
The work is positive (W+) if the force goes in the same direction of movement.
The work is negative (W-)if the force goes in the opposite direction to the movement
Net work (Wn)
Net work is defined as the sum of the work done from an initial place to an end point of the trajectory, for each of the individual forces to which the system is subjected.
Problem development
We determine the forces that perform work:
in formula (1 )we observe that the forces that perform work are the forces parallel to displacement. that is α = 0.
For this case they are the horizontal force (F) and the frictional force (Ff)
F=31.3 N : Horizontal force
Ff=μk*N , μk:coefficient of kinetic friction , N : Normal force
N=W
W: block weight W= m*g, m: block mass , g: acceleration due to gravity
W= 4.30 kg* 9.8 m/s² = 42.14 N
Ff= 0.599*42.14 N= 25.24 N : Frictional force
Calculating of the Net work (Wn)