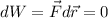Question

A 3.00-kg ball swings rapidly in a complete vertical circle of radius 2.00 m by a light string that is fixed at one end. The ball moves so fast that the string is always taut and perpendicular to the velocity of the ball. As the ball swings from its lowest point to its highest point, what is the work done by gravity and by the tension?

Answer 1

• The gravity does a work of - 117.6 Joules.

• The tension does not do work as the force is perpendicular to the direction of motion at any point in the trajectory.

Step-by-step explanation:

The work done by the gravity simply is the difference in gravitational potential energy multiplied by -1:

`W_g = - \Delta E_p = - (mgh_f  - m g h_i)`

where m is the mass of the ball, g is the acceleration due to gravity,
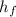`h_f` is the final height and
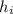`h_i` is the initial height.

So, if the radius is 2.00 m, then the difference of height will be 4 meters:

`W_g = - mg (h_f - h_i)`

`W_g = - 3.00 \ kg \ 9.8 (m)/(s^2) \ 4 \m`

`W_g = - 117.6 Joules`

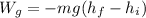
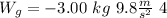
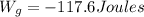
As the tension is perpendicular to the velocity of the ball, the force is always perpendicular to the direction of motion. So, the differential of work will be:

`dW = \vec{F}  d\vec{r} = 0`