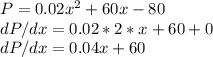Question

Let C(x) represent the cost of producing x items and p(x) be the sale price per item if x items are sold. The profit P(x) of selling x items is P(x)=xp(x)-C(x) (revenue minus costs). The average profit per item when x items are sold is P(x)/(x) and the marginal profit is dP/dx. The marginal profit approximates the profit obtained by selling one more item given that x items have already been sold. Consider the following cost functions C and price function p.C(x)=-0.02x^2+40x+80, p(x)=100, a=500a) what is the profit function P.P(x)=?b) find the average profit function and marginal profit function.average profit function: P(x)/(x)=?marginal profit function: dP/dx=?c

Answer 1

(a) Profit function P(x) = 0.02x^2+60x-80

(b) Average profit P(x)/x = P/x = 0.02x+60-80/x

Marginal profit dP/dx = 0.04x+60

Explanation:

Cost function: C(x) = -0.02x^2+40x+80

Price function: p(x) = 100

(a) The profit function P(x) = x*p(x)-C(x) can be expressed as:

`P=x*p-C\\P=x*100-(-0.02x^(2) +40x+80)\\P=0.02x^(2)+60x-80`

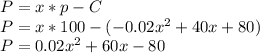
(b)Average profit function: P(x)/x

`P/x=(0.02x^(2)+60x-80)/x\\P/x = 0.02x+60-80/x`

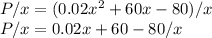
Marginal profit function: dP/dx

`P=0.02x^(2)+60x-80\\dP/dx=0.02*2*x+60+0\\dP/dx=0.04x+60`