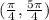Question

Consider the function on the interval (0, 2π). f(x) = sin(x) cos(x) + 8 (a) Find the open interval(s) on which the function is increasing or decreasing. (Enter your answers using interval notation.) increasing decreasing (b) Apply the First Derivative Test to identify all relative extrema. relative maxima (x, y) = (smaller x-value) (x, y) = (larger x-value) relative minima (x, y) = (smaller x-value) (x, y) = (larger x-value)

Answer 1

a) Increasing in

`(0,(\pi)/(4))`

`((5\pi)/(4),2\pi)`

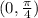
decreasing

`((\pi)/(4),(5\pi)/(4))`

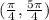
Local maximum

`(\pi)/(4)`

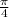
Local minimum

`(5\pi)/(4)`

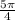
Explanation:

Let f(x) be

f(x) = sin(x)+cos(x)+0 for 0<x<2π.

Taking the first derivative

f'(x) = cos(x)-sin(x)

The critical points are those where the derivative vanishes.

f'(x) = 0 iif cos(x) = sin (x), so, the critical points in (0, 2π) are

`x=(\pi)/(4)\;and\; (5\pi)/(4)`

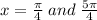
To find out what kind of critical points they are, we take the second derivative

f''(x) = -sin(x)-cos(x)

Evaluate this expression at the critical points

`f''((\pi)/(4))=-(\sqrt2)/(2)-(\sqrt2)/(2)< 0`

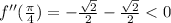
so, this point is a local maximum.

`f''((5\pi)/(4))=(\sqrt2)/(2)+(\sqrt2)/(2)> 0`

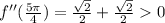
and here we have a local minimum.

The function then is increasing in the intervals

`(0,(\pi)/(4))\;and\;((5\pi)/(4),2\pi)`

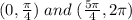
and decreasing in

`((\pi)/(4),(5\pi)/(4))`