Basis step: Let
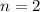 . Then
. Then

and
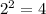
so
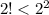 .
.
Inductive step: Assume
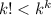 . We want to show that
. We want to show that
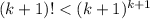 .
.
Now
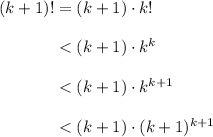
where the first inequality follows from the induction hypothesis; the second follows from multiplying the right side by some
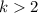 ; and the third from adding the remaining terms to complete the binomial expansion
; and the third from adding the remaining terms to complete the binomial expansion
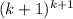 , all of which are positive since they are some power of
, all of which are positive since they are some power of
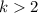 .
.
QED