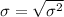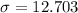Question

Listed below are the top 10 annual salaries​ (in millions of​ dollars) of TV personalities. Find the​ range, variance, and standard deviation for the sample data. Given that these are the top 10​ salaries, do we know anything about the variation of salaries of TV personalities in​ general?42 40 39 31 22 18 15 12 11.7 10.5(a) The Range of the sample data is _____ million. (Type an integer or a decimal)(b) The variance of the sample data is _____. (Round to three decimal places as needed.)

Answer 1

The Range of the sample data is 31.5 million.

The variance of the sample data is 161.377

The standard deviation is 12.703 million

Explanation:

The range of a sample is the result of the subtraction of the biggest value in the sample by the smallest.

In our sample, the biggest value is 42 million, while the smallest is 10.5 million.

So the range is:

42 - 10.5 = 31.5 million

The variance of a sample of size N is given by the following formula:

`\sigma^(2) = (1)/(N)\sum_(k=1)^(N) (x_(k) - M)^(2)`

where
`x_(k)` is the element at the position k of the set and M is the mean of the set.

So, to find the variance of this sample, first we have to find the mean.

The mean of a sample is the sum of the values of sample divided by the sample's size. There are 10 values, so:

`M = (42 + 40 + 39 + 31 + 22 + 18 + 15 + 12 + 11.7 + 10.5)/(10) = (241.2)/(10) = 24.12`

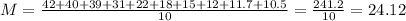
So, we have that:

`\sigma^(2) = (1)/(N)\sum_(k=1)^(N) (x_(k) - M)^(2)`

`\sigma^(2) = (1)/(10)((42 - 24.12)^(2) + (40 - 24.12)^(2) + (39 - 24.12)^(2) +(31 - 24.12)^(2) + (22 - 24.12)^(2) + (18 - 24.12)^(2) + (15 - 24.12)^(2) + (12 - 24.12)^(2) + (11.7 - 24.12)^(2) + (10.5 - 24.12)^(2))`

`\sigma^(2) = 161.377`

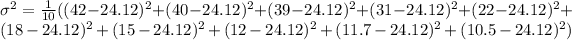
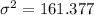
The standard deviation is the square root of the variance, so:

`\sigma = \sqrt{\sigma^(2)}`

`\sigma = √(161.377)`

`\sigma = 12.703`