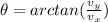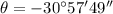Answer:
a. the magnitude of the speed is 14.69 m/s
b. The direction is - 30 ° 57' 49''
Step-by-step explanation:
As there are no external forces in the horizontal direction, we know that the linear momentum must be conserved.
So, taking
 our initial momentum and
our initial momentum and
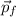 our final momentum, we got:
our final momentum, we got:

The momentum of the system will be:
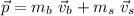
where
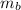 and
and
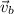 are the mass and the velocity of the bullet and
are the mass and the velocity of the bullet and
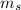 and
and
 are the mass and the velocity of the stone.
are the mass and the velocity of the stone.
Initial conditions
We know that the mass of the bullet is :
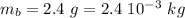
taking the unit vector
 pointing in the original direction of the bullet, the velocity will be:
pointing in the original direction of the bullet, the velocity will be:
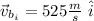
The mass of the stone is
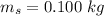
as is at rest, the initial velocity will be zero
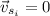
So, our initial momentum will be
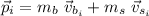
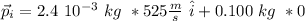
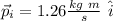
Final conditions
The masses will be the same.
Taking the unit vector
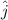 pointing in the final direction of the bullet, the velocity of the bullet is
pointing in the final direction of the bullet, the velocity of the bullet is
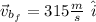
So, the final momentum will be


Obtaining the velocity
Now, we use

and we obtain
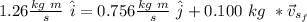
working it a little

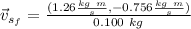
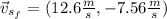
This is the final velocity of the stone. Now, we can obtain the magnitude using the Pythagorean theorem:
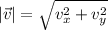
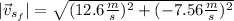
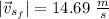
We can obtain the angle as: