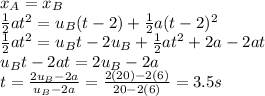Question

Traveler A starts from rest at a constant acceleration of 6 m/s^2. Two seconds later, traveler B starts with an initial velocity of 20 m/s at the same acceleration of 6 m/s^2. as measured by a, at what time will traveler B overtake traveler A?

a. 0.4s
b. 1.5s
c. 2.0s
d. 2.5s
e. 3.5s

Answer 1

3. 3.5 s

Step-by-step explanation:

The position of traveller A is given by the equation:

`x_A(t) = (1)/(2)a t^2`

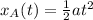
where

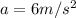`a = 6 m/s^2` is the acceleration of A

t is the time measured from when A started the motion

The position of traveller B instead is given by

`x_B(t) = u_B (t-2) + (1)/(2)a(t-2)^2`

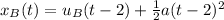
where a (acceleration) is the same as traveller A, and

`u_B = 20 m/s`

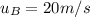
is B's initial velocity. We can verify that the formula is correct by substituting t=2, and we get
`x_B=0`, which means that B starts its motion 2 seconds later.

Traveller B overtakes traveller A when the two positions are the same, so:

`x_A = x_B\\(1)/(2)at^2 = u_B (t-2) + (1)/(2)a(t-2)^2\\(1)/(2)at^2 = u_B t - 2u_B +(1)/(2)at^2 +2a-2at\\u_Bt-2at = 2u_B-2a\\t=(2u_B-2a)/(u_B-2a)=(2(20)-2(6))/(20-2(6))=3.5 s`