Answer:
The perimeter of the rectangle is 17.70 feet
Explanation:
- The perimeter of a rectangle is → P = 2l + 2w → where l is its length
and w is its width
- A rectangle has a length 15x and a width 2x³ + 4 - 2x²
- We need to find its perimeter when its length is 5 feet
∵ The length of the rectangle is 15x
∵ The length of the rectangle is 5 feet
- Equate the length's expressions
∴ 15x = 5
- Divide both sides by 15
∴
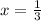
- Now lets find the width of the rectangle
∵ The width of the rectangle = 2x³ + 4 - 2x²
∵
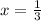
- Substitute the value of x in the expression of the width
∴
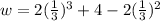
∴
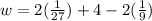
∴
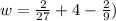
∴
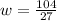 feet
feet
∵ l = 5 feet and
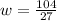 feet
feet
∵ P = 2l + 2w
∴ P = 2(5) +
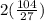
∴ P = 10 +
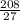
∴ P = 17.70 feet
* The perimeter of the rectangle is 17.70 feet