Question

Two stars have the same luminosity, but Star A is 10.0 times farther away than Star B. How much fainter does Star A appear compared to Star B? times fainter

Answer 1

B(A)100=B(B), the star A is 100 times fainter than star B.

Step-by-step explanation:

Brightness of the star is defined by the formula,

`B=(L)/(4\pi d^(2))`

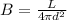
Here, L is the luminosity and d is the distance.

For star A, the distance is 10d. The brightness of star A.

`B(A)=(L)/(4\pi (10d)^(2))`

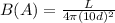
For star B, the distance is d. The brightness of star B.

`B(B)=(L)/(4\pi d^(2))`

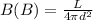
Now according to the question luminosity of two stars is equal.

Therefore,

`B(A){4\pi (10d)^(2)}=B(B){4\pi (d)^(2)}\\B(A)100=B(B)`

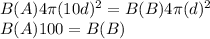
So, star B is 100 times brighter than star A.

Therefore the star A is 100 times fainter than star B.