Question

1. Find an equation of the plane. The plane through the points (0, 8, 8), (8, 0, 8), and (8, 8, 0)2. Find parametric equations and symmetric equations for the line. (Use the parameter t.) The line through(3, ?1, 5) and parallel to the line x + 4 = y/2 = z-53. Find the point at which the line intersects the given plane. x = 4 ? t, y = 2 + t, z = 5t; x ? y + 4z = 204. Determine whether the planes are parallel, perpendicular, or neither. 2x + 8y ? 6z = 1, ?15x + 30y + 35z = 0If neither, find the angle between them. (If the planes are parallel or perpendicular, enter PARALLEL or PERPENDICULAR, respectively.)

Answer 1

1. The equation of the plane is
`x+y+z-16=0`.

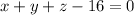2. The symmetric equation of the line is
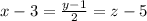`x-3=(y-1)/(2)=z-5`, and the parametric equation is

`r(t) = \begin{cases} x &= 3 + t\\ y &= 1 + 2t\\ z &= 5+ t\end{cases}`.

3. The intersection point is (-5,11,45).

4. The angle between the planes is 13.85° approximately.

Explanation:

1. Let us obtain the equation of the plane through the points A(0, 8, 8), B(8, 0, 8), and C(8, 8, 0). Recall that three points define a unique plane. The idea to find the asked equation is:

First: Find to vectors contained on the plane. Notice that the vector with endpoints at A and B is on the plane, and the one with endpoints at B and C. So, let us calculate those vectors

• 
  `\vec{u} = (8, 0, 8) -  (0, 8, 8) = (8,-8,0)`

• 
  `\vec{v} = (8, 8, 0) -  (8, 0, 8) = (0,8,-8)`

Second: Find the cross product of vectors
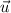`\vec{u}` and
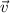`\vec{v}`, which is the normal vector to the plane,

`\begin{vmatrix} i & j & k\\ 8 & -8 & 0\\ 0 & 8 & -8\end{vmatrix} = i\begin{vmatrix} -8 & 0\\ 8 & -8\end{vmatrix} -j\begin{vmatrix} 8 & 0\\ 0 & -8\end{vmatrix} +k\begin{vmatrix} 8 & -8\\ 0 & 8\end{vmatrix} = 64i+64j+64k`

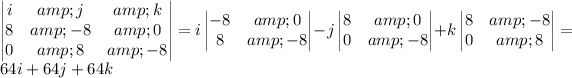
Third: We obtain the equation of the plane. With the normal vector we know that the plane has equation

`64x+64y+64z+D=0`.

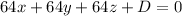In order to obtain the value of D we substitute any of the given points A, B or C. We choose in particular A:

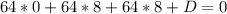`64*0+64*8+64*8+D=0` that gives
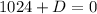`1024+D=0`, so
`D=-1024`.

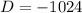The equation of the plane is [
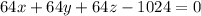`64x+64y+64z-1024=0`, but we can make the equation a little bit simpler if we divide the whole equation by 64:

`x+y+z-16=0`.

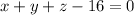2. In this exercise we assume that the point is P(3,1,5). Recall that to lines are parallel if they have the same direction vector. So, we need to find the direction vector of the line with equation x + 4 = y/2 = z-53.

Also, recall that given the symmetric equation of a line

`(x-x_0)/(A)=(y-y_0)/(B)=(z-z_0)/(C)`

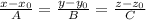
its direction vector is (A,B,C). So, in this exercise, the direction vector we are looking for is (1,2,1).

Now, we have all the information needed to give the equation of the line:

• a point on the line: P(3,1,5)
• the direction vector: v(1,2,1).

Symmetric equation: The symmetric equation of a line has the form

`(x-x_0)/(A)=(y-y_0)/(B)=(z-z_0)/(C)`

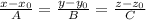
where (A,B,C) is the direction vector ans
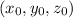`(x_0,y_0,z_0)` is a point on the line. So, substituting the data we have obtained:

`(x-3)/(1)=(y-1)/(2)=(z-5)/(1)`

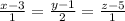
which is equivalent to

`x-3=(y-1)/(2)=z-5`.

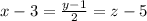Parametric equation: The parametric equation of a line has the form

`r(t) = \begin{cases} x &= x_0 + At\\ y &= y_0 + Bt\\ z &= z_0 + Ct\end{cases}`

where (A,B,C) is the direction vector ans
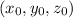`(x_0,y_0,z_0)` is a point on the line. So, substituting the data we have obtained:

`r(t) = \begin{cases} x &= 3 + t\\ y &= 1 + 2t\\ z &= 5+ t\end{cases}`.

3. In this exercise we assume that equation of the line is

`s(t) = \begin{cases} x &= 4 + t\\ y &= 2 + t\\ z &= 5t\end{cases}`

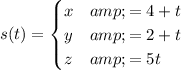
an the plane has equation
`x + y + 4z = 204`.

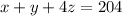The idea in this kind of exercise is to substitute the values of x, y and z given by the parametric equation of the line into the equation of the plane. What we get with operation is a linear equation on t.

Then,

`(4+t) + (2+t) +4(5t) = 204`

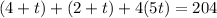
which is equivalent to
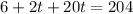`6 +2t+20t=204`. Then,
`22t=198` and

`t=9`.

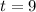Now, we substitute this value of t in the parametric equation of the line:

`s(9) = \begin{cases} x &= 4 - 9\\ y &= 2 + 9\\ z &= 5*9\end{cases}`

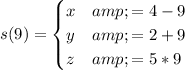
and the intersection point is (-5,11,45).

4. In this exercise we assume that the equations are
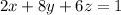`2x + 8y + 6z = 1` and
`15x + 30y + 35z = 0`.

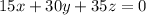We study the angle between two planes making the dot products of their normal vectors. Recall that a plane with equation

`Ax+By+Cz+D=0`

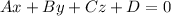
its normal vector is (A,B,C).

So, in this case we have that the normal vectors are v(2,8,6) and u(15,30,35). The dot product gives

`u\cdot v = 30 + 240 + 210 = 480 \\eq 0`.

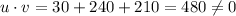Then, they are not perpendicular. Moreover, they are not parallel because they are not proportional (
`2/6 \\eq 8/30`).

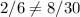To find the angle we use the formula:

`\cos\alpha = (u\cdot v)/(|u||v|)`.

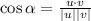So we must calculate the length of the vectors:

• 
  `|v| = √(2^2+8^2+6^2) = √(4+64+36)=√(104) = 2√(2\cdot 13)`

• 
  `|v| = √(15^2+30^2+35^2) = √(225+900+1225)=√(2350) = 5√(2\cdot 47)`

Then,

`\cos\alpha = (u\cdot v)/(|u||v|) =(480)/(2√(2)√(13)5√(2)√(47)) = (24)/(√(13)√(47)) \approx 0.97093607287`.

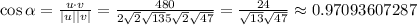To obtain the angle between the plane we use the inverse cosine function

`\alpha = \arccos(0.97093607287) =13.847529^\circ \approx 13.85^\circ`.