Step-by-step explanation:
Relation between gauge pressure and density and height is as follows.
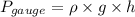
The given data is as follows.
 = 1025
= 1025
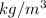
g = 9.81
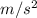
h = 2.5 m
Therefore, substitute the given values into the above formula as follows.
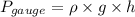
=
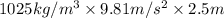
=
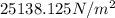
or, =
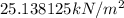
= 25.138125 kPa
Thus, we can conclude that the gauge pressure exerted by sea-water is 25.138125 kPa.