Question

Two beetles run across flat sand,starting at the same point. beetle 1 runs 0.50 m due east,then 0.80 m at 30° north of due east. beetle 2 also makes two runs; the first is 1.6 m at 40° east of due north.what must be (a) the magnitude and (b) the direction of its second run if it is to end up at the new location of beetle 1?

Answer 1

(a) 0.85 m

Let's start by analyzing the motion of beetle 1. We need to resolve its motion along two directions: east-west (x-direction) and north-south (y-direction).

`A_x = 0.50 + 0.80 cos 30^(\circ) =1.19 m`

`A_y = 0.80 sin 30^(\circ) =0.40 m`

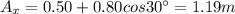
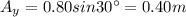
Now let's do the same with beetle 2:

`B_x = 1.60 sin 40^(\circ)+ x_2 = 1.03 + x_2`

`B_y = 1.60 cos 40^(\circ) + y_2 = 1.23 + y_2`

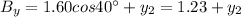
where
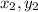`x_2,y_2` are the components of the second run of beetle 2, which are unknown.

We want beetle 2 to end up at the same location of beetle 1, so the x- and y- component of the displacement of the two beetles must be the same. Therefore:

`A_x = B_x\\1.19 = 1.03 + x_2 \rightarrow x_2 = 1.19-1.03 = 0.16 m`

`A_y = B_y \\0.40 = 1.23+ y_2 \rightarrow y_2 = 0.40-1.23 = -0.83 m`

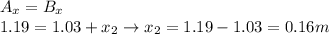
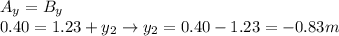
So, the magnitude of the displacement of the second run of beetle 2 must be

`d=√(x_2^2+y_2^2)=√(0.16^2+(-0.83)^2)=0.85 m`

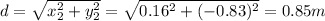
(b)
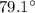`79.1^(\circ)` south of east

In order to find the direction of the second run of beetle 2, let's consider again the components of this displacement:

`x_2 = 0.16 m\\y_2 =-0.83 m`

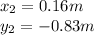
We can find the direction by using the formula

`tan \theta = (y_2)/(x_2)`

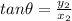
By substituting,

`tan \theta = (-0.83)/(0.16)=-5.188\\\theta = tan^(-1)(-5.188)=-79.1^(\circ)`

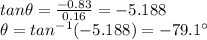
which means
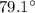`79.1^(\circ)` south of east.