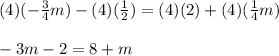Question

Which number can each term of the equation be multiplied by to eliminate the fractions before solving? m – negative StartFraction 3 Over 4 EndFraction m minus StartFraction one-half EndFraction equals 2 StartFraction one-fourth EndFraction m. = 2 + m 2 3 4 5

Answer 1

The Answer is 4

Explanation:

I just did the Quiz on Edge

Answer 2

Answer: Each term of the equation can be multiplied by
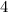`4` to eliminate the fractions before solving.

Explanation:

Given the following expression:

`-(3)/(4)m-(1)/(2)=2+(1)/(4)m`

You need to simplify before solve it.

Notice that the denominators are different, then you must find the Least Common Denominator (LCD).

Descompose the denominators into their prime factors:

`4=2*2=2^2\\2=2`

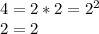
Choose
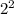`2^2`, because it has the highest exponent. Then:

`LCD=2^2=4`

Finally you can multiply on both sides by 4 in order to to eliminate the fractions before solving:

`(4)(-(3)/(4)m)-(4)((1)/(2))=(4)(2)+(4)((1)/(4)m)\\\\-3m-2=8+m`