Question

Imagine you are a newly hired Air Force engineer working on Kirtland Air Force Base. You have been tasked with a few of the design elements for the jet fuel storage tank system. You have a 30-ft tall cylindrical tank with a diameter of 15 ft, which has been filled to 20 ft with Jet A (p 6.71 lbm/gal). (a) Calculate the hydrostatic pressure at the bottom of the tank. Give your answer in psig (b) Calculate the total force exerted on the vertical walls of the tank due to hydrostatic pressure. Give your answer in lbf.

Answer 1

(a) The pressure at the bottom of the tank is 6972 psig.

(b) The force exerted in the vertical walls of the tank is 473,109,880 lbf.

Step-by-step explanation:

(a) We can define the hydrostatic pressure of the bottom of the tank as the weight of the column of fuel:

`P=\rho*g*h\\P=6.71(lbm)/(gal)*32.17405(ft )/(s^(2))*20ft*(7481gal)/(1ft3)   *(1lbf)/(1lbm*32.17405(ft )/(s^(2)))  *((1ft)/(12in))^(2)\\\\P=6972 lbf/in^(2)=6972psig`

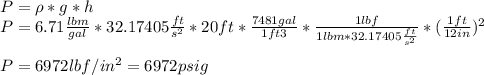
The pressure at the bottom of the tank is 6972 psig.

(b) The force exerted on the vertical walls is equivalent to the pressure at every depth of the tank multiplied by the surface area.

In this case, the force is exerted from the bottom to 20 ft high in the tank.

The pressure rise linearly with depth, so we can calculate an average pressure like

`\bar{P}=(P_(20ft)+P_(0ft))/2=(0+6972)/2 psig=3486 psig`

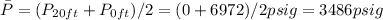
The surface area of the tank lateral walls is

`S=(\pi*D)*h=(3.1416*15ft)*20ft=942,48 ft^(2)`

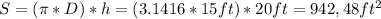
We only considered up to 20 ft beacuse is the only part of the wall where forces are applied. It has to be coherent with the pressure consedered (from 0 to 20 ft).

Then we can calculate the force as

`F=P*S=3486(lbf)/(in^(2) ) *942.48ft^(2) *((12in)/(1ft) )^(2)= 473,109,880 lbf`

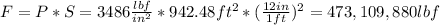
The force exerted in the vertical walls of the tank is 473,109,880 lbf.