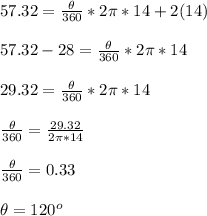Question

If the radius is 14cmand The perimeter of the sector is 57.32cm.

what is the size of the angle?​

Answer 1

120°

Explanation:

A sector of a circle is the portion or region of a circle enclosed by two radii and an arc. The perimeter of a the sector of a circle is given by the formula:

Perimeter of sector =
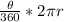`(\theta)/(360) *2\pi r` + 2r

Where θ is the angle which forms the sector and r is the radius of the circle.

Given that Perimeter of sector = 57.32 cm, radius (r) = 14 cm, we can find the angle θ using:

Perimeter of sector =
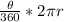`(\theta)/(360) *2\pi r` + 2r

`57.32=(\theta)/(360) *2\pi *14+2(14)\\\\57.32-28=(\theta)/(360) *2\pi *14\\\\29.32=(\theta)/(360) *2\pi *14\\\\ (\theta)/(360)=(29.32)/(2\pi *14) \\\\(\theta)/(360)=0.33\\\\\theta=120^o`