Question

Can someone show me how to de problem number 10 11 ASAP PLEASE

Answer 1

Remove square roots by taking squares:

10.

`√(3x+10)=5-2x`

`(√(3x+10))^2=(5-2x)^2`

`3x+10=25-20x+4x^2`

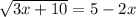
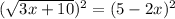
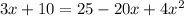
Keep in mind that
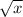`\sqrt x` is defined as long as
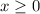`x\ge0`; in this case, we require
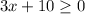`3x+10\ge0`, or
`x\ge-\frac{10}3`.

`4x^2-23x+15=0`

`(4x-3)(x-5)=0`

`4x-3=0\text{ or }x-5=0`

`x=\frac34\text{ or }x=5`

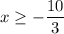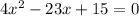
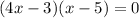
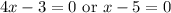
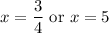
Both of these solutions are greater than -10/3, so they are both valid.

11.

`4x=√(1-6x)`

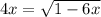
This tells us we need to have
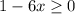`1-6x\ge0`, or
`x\le\frac16`.

`(4x)^2=(√(1-6x))^2`

`16x^2=1-6x`

`16x^2+6x-1=0`

`(8x-1)(2x+1)=0`

`8x-1=0\text{ or }2x+1=0`

`x=\frac18\text{ or }x=-\frac12`

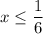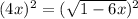
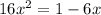
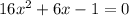
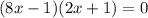
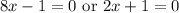
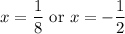
Both of these are valid solutions.