Answer:
Brightness of sun surface = 2.2045 times of brightness of sunspot
Step-by-step explanation:
We have given temperature of sunspot
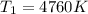
Temperature of solar surface

Now according to Stefan's law
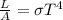 , here L is radiated power, A is area,
, here L is radiated power, A is area,
 is stefan constant
is stefan constant
As the brightness depends on the radiated power
So
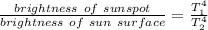
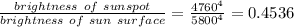
Brightness of sun surface = 2.2045 times of brightness of sunspot