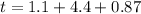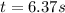Question

A car and a truck are both traveling at the constant speed of 35 mi/h; the car is 40 ft behind the truck. The driver of the car wants to pass the truck, i.e., he wishes to place his car at B, 40 ft in front of the truck, and then resume the speed of 35 mi/h. The maximum acceleration of the car is 5 ft/s2 and the maximum deceleration obtained by applying the brakes is 20 ft/s2. What is the shortest time in which the driver of the car can complete the passing operation if he does not at any time exceed a speed of 50 mi/h

Answer 1

t = 6.37 s

Step-by-step explanation:

If we see the motion of car with respect to truck then

relative speed of car initially and finally is ZERO

maximum relative speed of car could be

`v_(max) = 50 - 35 = 15 mph`

`v_(max) = 6.7 m/s`

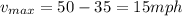
now maximum acceleration of the car is given as

`a_(max) = 5 ft/s^2 = 1.524 m/s^2`

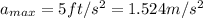
maximum deceleration is given as

`a_(max) = 20 ft/s^2 = -6.096 m/s^2`

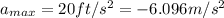
now car has to cover the relative separation of 80 ft

`d = 24.2 m`

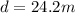
now we have

distance covered to stop the car from maximum speed is

`v_f^2 - v_i^2 = 2 a d`

`0 - 6.7^2 = 2(-6.096)d`

`d_2 = 3.68 m`

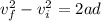
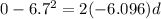
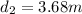
time taken to cover this distance

`t_2 = (v)/(a) = (6.7)/(6.096)`

`t_2 = 1.1 s`

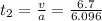
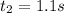
now distance cover to reach maximum speed

`d_1 = (v_f^2 - v_i^2)/(2a)`

`d_1 = (6.7^2)/(2(1.524))`

`d_1 = 14.7 m`

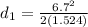
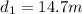
time taken to cover this distance

`t_1 = (v)/(a) = (6.7)/(1.524)`

`t_1 = 4.4 s`

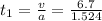
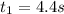
now remaining distance is covered at constant speed

`t_2 = (24.2 - 3.68 - 14.7)/(6.7)`

`t_2 = 0.87 s`

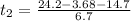
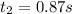
So total time is

`t = 1.1 + 4.4 + 0.87`

`t = 6.37 s`