Question

A particular group of men have heights with a mean of 174 cm and a standard deviation of 6 cm. Earl had a height of 192 cm. a. What is the positive difference between Earl​'s height and the​ mean? b. How many standard deviations is that​ [the difference found in part​ (a)]? c. Convert Earl​'s height to a z score. d. If we consider​ "usual" heights to be those that convert to z scores between minus2 and​ 2, is Earl​'s height usual or​ unusual? a. The positive difference between Earl​'s height and the mean is nothing cm.

Answer 1

a) 18 cm

b) 18

c) 3

The Earl's height is unusual because the z score does not lies in the given range of usual i.e -2 and 2

Explanation:

Given:

Mean height, μ = 174 cm

Standard deviation = 6 cm

height of Earl, x = 192 cm

a) The positive difference between Earl height and the mean = x - μ

= 192 - 174 = 18 cm

b) standard deviations is 18

c) Now,

the z score is calculated as:

`z=(x-\mu)/(\sigma)`

or

`z=(192-174)/(6)`

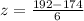
or

z = 3

The Earl's height is unusual because the z score does not lies in the given range of usual i.e -2 and 2