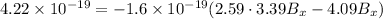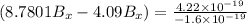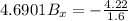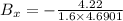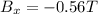Answer:
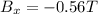
Explanation:
We are given that an electron moves through a uniform magnetic field given by
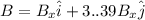
Velocity of electron=
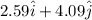 m/s
m/s
Magnetic force acting on electron, F=
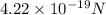
We have to find
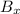
Charge on electron=q=
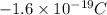
We know that magnetic force on electron is given by
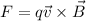
Substitute the value then we get