Question

The isotope 'Sr has a half-life of 28.8 years. What is the activity, measured in atoms/second, of a 50 mg sample of "Sr? (10 pts.)

Answer 1

The activity of 50mg of Sr is
`2.63x10^(11) atoms/second`

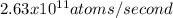
Step-by-step explanation:

Every nuclear disintegration follows the first order rate, thus the half-life (t1/2) is
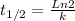`t_(1/2) =(Ln 2)/(k)` where k is the constant of the reaction.

Considering 1 year equals 3.15x107 seconds

`(28.8year x.3.15x10^(7)s )/(1 year) = 9.072x10^(8) s`

For Sr with t1/2 =
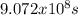`9.072x10^(8) s` , the constant of the reaction is

`k =(Ln 2)/(t_(1/2))=(Ln 2)/(9.072x10^(8) s ) = 7.64x10^(-10) s^(-1)`

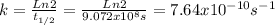
The activity (A) of a nucleus is
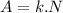`A = k.N` where N is the number of nucleus. Sr molecular mass is 87.6g/mol and every mol contains 6.023x1023 atoms, thus

`(50x10^(-3)g x 6.022x10^(23) atoms)/(87.6g) = 3.44x10^(20) atoms`

Therefore, the activity of 50mg of Sr is

`A = k.N = 7.64x10^(-10) s^(-1) x 3.44x10^(20)atoms = 2.63x10^(11) atoms/second`