Question

A light plane must reach a speed of 46 m/s for takeoff.

How long of a runway is needed if the (constant) acceleration is 3.2 m/s2 (units)

Answer 1

The plane will need 330.63m of runway for takeoff.

Why?

Since we already know the desired speed (46 m/s) of the plane and we know its acceleration (constant acceleration, 3.2 m/s2), we can calculate how much runway is needed for takeoff.

We can solve the problem using the following formula:

`V^(2)=V_(o)^(2) +2a*d`

`d = ((V^(2)  - Vo^(2) ))/(2a)`

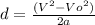
Where,

V is the final speed

Vo is the initial speed (which is equal to 0 assuming that the plane was in rest)

a is the acceleration of the movement.

d is the distance.

Now, substituting the given information and calculating, we have:

`(46(m)/(s) )^(2)=(0)^(2) +2*(3.2(m)/(s^(2) )) *d\\\\2116(m^(2))/(s^(2))=2*(3.2(m)/(s^(2) ))*d\\\\2116(m^(2))/(s^(2))=6.4(m)/(s^(2) )*d\\\\d=(2116(m^(2))/(s^(2)))/(6.4(m)/(s^(2) ))=330.63m`

Hence, we have that the plane will need 330.63m of runway for takeoff.

Have a nice day!